Identificacion del equipo de trabajo
Fecha realización consulta: (a continuación por favor, escriba la fecha de consulta)
Fecha socialización: (a continuación por favor, escriba la fecha de socialización)
Tema: Ondas estacionarias
Objetivo: el estudiante estará en capacidad de expresar con coherencia y claridad en qué consiste el fenómeno de ondas estacionarias en una columna de aire.
Dinámica de la actividad: responda el cuestionario de 16 preguntas, después de estudiar y entender la información que se presenta a continuación y complementar si es necesario consultando respecto a las oscilaciones de una cuerda tensa en la bibliografía y web grafía recomendadas.
Análogamente a como se producen las ondas estacionarias en una cuerda, se producen las ondas estacionarias en una columna de aire confinado en un tubo por la superposición de ondas longitudinales incidentes y reflejadas en el interior del mismo tubo en estado de resonancia. En una columna de aire los modos propios de oscilación no se pueden ver a simple vista como sucede en una cuerda; los modos propios existen como arreglos de las moléculas de aire llamados condensaciones y rarefacciones.
La función de onda en estado estacionario para una columna de gas confinada dentro de un tubo de longitud finita, así como para el caso de la cuerda (1), puede escribirse en términos de la ecuación:
ψ(x, t) = (Asen (kx) + Bcos (kx)) senωt
Las frecuencias de resonancia fn correspondientes a los distintos modos de oscilación de la columna de aire, se obtienen de la misma manera como se consideró en la cuerda tensa, aplicando las diferentes condiciones de frontera. Estas determinan la condición del tubo, el cual puede ser:
a) abierto en ambos extremos b) abierto (en un extremo) c) cerrado (en ambos extremos)
a) Tubos abiertos en ambos extremos
Cuando las condiciones de frontera son:
• ∂ψ (x ,t) /∂x |x=0 = 0; • ∂ψ (x,t) /∂x |x=L = 0;
Lo que significa que en x = 0 y en x = L, las moléculas de aire tienen un valor máximo de desplazamiento a partir de su posición de equilibrio, definiendo un tubo abierto en ambos extremos.
Las frecuencias de resonancia correspondientes a los distintos modos propios de oscilación de la columna de aire en un tubo abierto en ambos extremos se encuentran aplicando estas condiciones de frontera en forma análoga a como se hizo para el caso de ondas estacionarias en la cuerda:
fn = (n* vs /2L); para n = 1, 2, 3... (ecuación 1)
Donde vs es la velocidad del sonido en el aire. En un tubo abierto existen todos los sobre-tonos posibles matemáticamente por lo que se corresponden con los armónicos y las frecuencias de resonancia fn también se conocen con el nombre de armónicos.
Los tubos abiertos entran en resonancia con un sonido cuando su longitud es un múltiplo de λ/2
En un tubo abierto el aire vibra con su máxima amplitud en ambos extremos.
Para un tubo abierto de longitud L, como la distancia entre dos nodos o entre dos vientres es media longitud de onda se tiene que:
L=λ/2; L=2λ2; L=3λ/2 L=4λ/2; L=5λ/2...
en general: L=n λ/2, para n=1, 2, 3, 4, 5... un número entero
Considerando que : λ=Vs/f (velocidad del sonido dividido por la frecuencia)
Las frecuencias de los distintos modos de vibración se pueden expresar como:
fn = n* vs /2L; con n = 1, 2, 3, …
n = 1 corresponde al modo fundamental: f1 = (1/2L) * vs;
n = 2 corresponde al segundo armónico: f2 = (2/2L) * vs
n = 3 corresponde al tercer armónico: f3= (3/2L) * vs
y así sucesivamente, siendo cada uno de ellos múltiplos de la frecuencia fundamental en la forma:
fn = n* vs /2L= n* f1; con n = 1, 2, 3, …
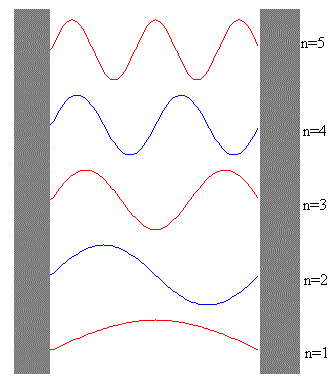
También n es el número de vientres de las ondas estacionarias (ver representación gráfica en los apuntes de clase de la semana de septiembre 21 a 27).
b) Tubos abiertos en un extremo (entiéndase cerrado en un extremo)
Si se considera un tubo de diámetro interior Φ, abierto en uno de los extremos y cerrado en el otro, con longitud que tal que se pueda aumentar y disminuir y por la boca abierta entra una onda sonora, de frecuencia determinada, el volumen del sonido aumenta y disminuye a medida que se hace variar la longitud del tubo. Ello se debe a que la onda sonora que entra en el tubo se refleja en la pared y cuando la onda que entra (onda incidente) y la reflejada están en fase el sonido se refuerza, se logra producir una onda estacionaria en el interior del tubo, esto solo ocurre cuando la longitud del tubo es un múltiplo impar de λ/4 (λ/4, 3λ/4, 5λ/4,7 λ/4, 9λ/4,11 λ/4, etc.). En esos casos se dice que el foco emisor del sonido y la columna de aire del interior del tubo están en resonancia.
Puede decirse que cuando las condiciones de frontera son:
• ∂ψ (x ,t) /∂x |x=0 = 0; • ∂ψ (x,t) /∂x |x=L = 0, para L variable;
Lo que significa que en x = 0 las moléculas de aire tienen un valor nulo de desplazamiento permaneciendo en su posición de equilibrio, y en x = L, las moléculas de aire tienen un valor máximo de desplazamiento a partir de su posición de equilibrio, definiendo un tubo abierto en un extremo.
Las frecuencias de resonancia correspondientes a los distintos modos propios de oscilación de la columna de aire en un tubo abierto en un extremo se encuentran aplicando estas condiciones de frontera en forma análoga a como se hizo para el caso de ondas estacionarias en la cuerda:
fn = (n* vs /4L); para n = 1, 3, 5, 7, 9... (ecuación 2)
como λ= vs /f (velocidad del sonido en el aire dividido por la frecuencia) se pueden obtener las frecuencias de los distintos modos de vibración representadas por la ecuación 2’ considerando L=(2n+1)*λ/4; para n=0, 1, 2, 3...Lo que también puede expresarse como:
f = (2n+1) * vs / 4L; para n = 0, 1, 2, 3, … (ecuación 2’)
En un tubo abierto en un extremo se debe aplicar corrección a la longitud del tubo:
L ’= L +0,8d; (ecuación 3)
En un tubo abierto en un extremo existen todos los sobre-tonos posibles matemáticamente por números enteros impares lo que implica que no se corresponden con los armónicos por lo que las frecuencias de resonancia fn no son los mismos armónicos.
c) Tubos cerrados (entiéndase cerrados en ambos extremos)
Cuando las condiciones de frontera son:
• ∂ψ (0,t) /∂x |x=0 = 0; • ∂ψ (L, t) /∂x |x=L = 0
Lo que significa que en x = 0 y en x = L las moléculas de aire tienen un valor nulo de desplazamiento permaneciendo en su posición de equilibrio, definiendo un tubo cerrado en ambos extremos.
Las frecuencias de resonancia correspondientes a los distintos modos propios de oscilación de la columna de aire en un tubo cerrado en ambos extremos encuentran aplicando estas condiciones de frontera en forma análoga a como se hizo para el caso de ondas estacionarias en la cuerda:
fn = (n* vs /2L); para n = 1, 2, 3, 4, 5, 6, 7, 8, 9... (ecuación 4)
En un tubo cerrado (en ambos extremos) se debe aplicar corrección a la longitud del tubo:
L ’= L +0,4d; (ecuación 3’)
Algunos ejemplos que ponen de manifiesto el fenómeno de resonancia son:
-Dos diapasones idénticos y próximos. Si el uno se hace vibrar el otro comienza a vibrar, esto se debe a que al ser idénticos vibran con la misma frecuencia y por tanto entran en resonancia.
-Los instrumentos de viento, por ejemplo las trompetas no suenan de cualquier forma, para que al soplar emitan una nota se tiene que cumplir que la vibración de los labios tengan una frecuencia capaz de producir resonancia con el aire que hay en el interior del tubo.
Ideas básicas
A continuación se concretan y completan algunas ideas básicas del tema que se estudia. Debe consultar las que están pendientes e intentar parafrasearlas todas para mejorar su capacidad de interpretación, comprensión y expresión en general.
Frecuencia en función de número de vientres n y longitud L, para Tubos sonoros
Abiertos en ambos extremos: fn = (n*/ 2L)* vs; para n=1, 2, 3, 4, 5…
Cerrados (en ambos extremos): fn = (n/2L)* vs; para n=1, 2, 3, 4, 5…
Abiertos en un extremo (cerrado en un extremos): fn = (n/ 4L)* vs; para n=1, 3, 5…
Un cuerpo vibrante produce sonido, el sonido requiere de un medio material para su propagación; el sonido no se propaga en el vacío.
El sonido se propaga por un movimiento de onda longitudinal de compresión y expansiones alternas. La longitud de onda es la distancia que hay entre una compresión y la otra consecutiva.
Las ondas sonoras producen modelos de interferencia.
El sonido produce ondas estacionarias en una columna de aire.
La reflexión del sonido produce un eco.
El sonido se puede reflejar, refractar y difractar.
La reflexión consiste en (por favor consulte y complete)______________________________
La refracción consiste en (por favor consulte y complete)______________________________
La difracción consiste en (por favor consulte y complete)______________________________
La resonancia ocurre cuando un cuerpo tiene una frecuencia natural igual a la frecuencia de una onda sonora.
Las notas musicales de una escala diatónica se reconocen por su tono.
El tono de una nota depende solamente de la frecuencia de vibración de la fuente. Dos notas que están en una octava de distancia tienen frecuencia de razón 2:1.
El intervalo musical entre dos notas es la razón de las frecuencias.
La intensidad de una nota depende de la amplitud de la onda sonora.
La calidad de una nota depende de los armónicos que un instrumento puede producir (sobre-tonos).
Las pulsaciones se escuchan cuando se tocan dos notas de aproximadamente la misma frecuencia, la frecuencia de las pulsaciones es f1-f2.
Una cuerda vibrante presenta un movimiento de onda estacionario.
La nota fundamental de una cuerda suena cuando λ/2 = L.
Hay producción de armónicos cuando L = λ; L = 3 λ /2; L = 4 λ/2, L = 5 λ/2, L = 6 λ/2, L = 7 λ/2, L = 8 λ/2, etc. (son las posibilidades matemáticas)
Un sonómetro se usa para medir el efecto de la longitud y la tensión en el tono de una cuerda.
El tono de una cuerda depende de su longitud L, la tensión T, y la masa por unidad de longitud m:
f α (1/L)(T/√m); α es el símbolo “proporcional a”
La nota fundamental de una columna de aire vibrante en un tubo abierto en un extremo suena cuando L = λ / 4.
Hay producciones de sobre-tonos en una columna de aire vibrante para un tubo abierto en un extremo (cerrado en un extremo), cuando
L = 2 λ / ; 4L = 3 λ / 4, L = 5λ / 4, L = 7λ / 4, L = 9λ / 4, etc.
Hay producciones de sobre-tonos en una columna de aire vibrante para un tubo abierto en ambos extremos, cuando
L = λ, L = 3 λ / 2, L = 4 λ / 2, L = 5 λ / 2, L = 6 λ / 2, L = 7 λ / 2, L = 8 λ / 2, L = 9 λ / 2, etc.
Cuestionario ACTIVIDAD 3
El cuestionario consta de 16 numerales, los cuales puede resolver después de estudiar la orientación teórica y completar las consultas indicadas.
1. Ilustre gráficamente los patrones de resonancia para ondas de presión en tubos abiertos y cerrados. (Sug. consulte los apuntes de clase de la semana Septiembre 21 a 27)
2. Explique la relación existente entre las ondas de desplazamiento y las ondas de presión en una columna de aire.
3. Calcule la frecuencias de resonancia para los primeros cinco modos de oscilación de la columna de aire en un tubo abierto en un extremo y en un tubo cerrado, utilizando las ecuaciones (2), (3) y 4. (Sug. tenga en cuenta las correcciones de la longitud del tubo: L ’= L +0,8d (ecuación 3); L ’= L +0,4d (ecuación 3’) respectivamente) .
4. Explique gráficamente los modos de resonancia de una columna de aire en:
a) un tubo abierto en un extremo b) un tubo cerrado (en ambos extremos)
(Sug. consulte los apuntes de clase de la semana Septiembre 21 a 27)
5. Considérese un tubo al cual se le puede variar la longitud, si la columna de aire dentro del tubo vibra en el modo fundamental o en el segundo armónico, ¿cómo es la relación entre frecuencia f y la longitud del tubo? Cuando:
a) el tubo es cerrado b) el tubo es abierto
Construya un gráfico en papel milimetrado de frecuencia f en función de 1/L para cada caso. ¿cómo es esta relación? (Sug. grafique para tubo abierto en ambos extremos, tubo cerrado en ambos extremos, tubo cerrado en un extremo)
6. Construya en papel milimetrado una gráfica de frecuencia f en función del número de vientres n en:
a) un tubo cerrado b) un tubo abierto en un extremo
Para cada caso: ¿Qué clase de curva obtiene? ¿Cómo varía la frecuencia en función de los vientres?
7. ¿Cómo escribiría la relación de comportamiento de la frecuencia en función de las variables discutidas en los pasos anteriores?
8. Tema libre. Consulte y exprese un término diferente a los que aparecen en las actividades propuestas
9. Para cada configuración del tubo (abierto en un extremo y cerrado) con las condiciones:
L = 90cm; diámetro d = 31mm
a) calcule la frecuencia de resonancia más baja (L = λ/2),
b) halle frecuencias superiores (deberá multiplicar la frecuencia calculada más baja por números enteros)
(Sug. aplique las respectivas fórmulas para la corrección de la longitud de cada tubo)
10. ¿Es la serie de números que usted ha calculado en el paso anterior el mismo para tubo cerrado que para tubo abierto en un extremo?
11. ¿Qué configuración de tubo dará una serie consecutiva de números enteros?
13. ¿Qué analogía encuentra entre las ondas estacionarias de una cuerda y las ondas estacionarias en tubos abiertos en un extremo y cerrados?
14. ¿Qué interpretación física tienen los modos propios de oscilación en tubos abiertos en un extremo y cerrados?
15. Compare la velocidad del sonido en sólidos, líquidos y gases. Explique por qué son diferentes.
16. Consulte aplicaciones de ondas estacionarias en una columna de aire.
Forma de realización: con excelente presentación y letra legible a mano, con una extensión máxima de tres renglones por cada término.
Modalidad: grupal
Forma de entrega: registrar en papel a mano con excelente preserntacion, buena ortografía y redacción; además socializar en el salón de clase.
Fecha máxima de entrega: la acordada en el salon de clase
NOTA: es recomendable realizar cada actividad dentro de la fecha establecida, ello implica un poco de auto-disciplina, un poco de responsabilidad y un poco de interés; además ayuda al estudiante para mejorar su capacidad de interpretar apropiadamente la información y adquirir nociones generales con cierta claridad sobre los temas programados, fortalecer su autonomía, su organización, su administración adecuada del tiempo y lograr mejor rendimiento académico en su proceso en general.
BIBLIOGRAFIA
(1) FISICA volumen II: campos y ondas Alonso-Finn, sección 22.5
Además los textos referenciados en el tema Bibliografía los cuales se encuentran en la biblioteca de la institución
WEBGRAFIA
Visite la menos uno de los enlaces referenciados
-Ondas estacionarias en una columna de aire en un tubo abierto
http://www.youtube.com/watch?v=qEULHxsUz5w
-Ondas estacionarias en una columna de aire en un tubo cerrado
http://www.youtube.com/watch?v=IFTA9AmXyuE&feature=related
Ondas estacionarias en una columna de aire
http://exa.unne.edu.ar/depar/areas/fisica/electymagne/TEORIA/ondas/estacionarias/estacionarias.html
xtr-10,2