Actividad 2. Ondas estacionarias en una cuerda tensa. Orientación teórica 3.

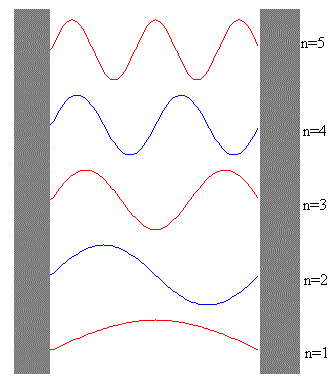
figura 1

Orientación teórica 3 . Brinda el referente teórico para realizar el laboratorio virtual 1. Ondas estacionarias en una cuerda tensa.  

 Equipo de trabajo: (por favor escriba la identificación del equipo corresondiente que realizó la actividad)

Fecha realización consulta: (por favor escriba la fecha en realizó la consulta)

Fecha socialización:(escriba la fecha) 

Tema: Ondas estacionarias 

Objetivo: el estudiante estará en capacidad de expresar con coherencia y claridad en qué consiste el fenómeno de ondas estacionarias en una cuerda tensa que vibra

Dinámica de la actividad: responda el cuestionario de 16 preguntas, después de estudiar y entender la información que se presenta a continuación y complementar si es necesario consultando respecto a las oscilaciones de una cuerda tensa en la bibliografía y web grafía recomendadas.

Considérese una cuerda de longitud L y densidad lineal de masa μ, sujeta en los extremos x = 0 y x = L.

Si la cuerda se hace oscilar en un punto arbitrario intermedio entre sus dos extremos fijos por medio de un vibrador conectado a un generador de ondas senoidales, conformará un oscilador forzado. Un análisis de las ondas incidentes y reflejadas que se forman en la cuerda (1) lleva a la siguiente función de onda como solución de la ecuación diferencial unidimensional de onda:

Ψ (x, t) = (A sen kx + B cos kx) senωt (ecuación 1)

Claramente ψ (x, t) no describe una onda viajera ya que x y t no están involucrados en el argumento de esta función en la forma (x ± v t). Esto da como resultado una amplitud que tiene la característica de ser fija para cada punto particular de la cuerda, pero variable de un punto a otro a lo largo de la misma. La expresión para la amplitud será entonces:

ψ (x, t) = (A sen kx + B cos kx) (ecuación 2)

Las constantes A y B se determinan con las condiciones iniciales.

Así la expresión:

ψ (x, t) = Φ(x) senωt

indica que cada punto de la cuerda tiene un movimiento armónico transversal de frecuencia ω.

Cuando la cuerda esté en resonancia con el agente externo que produce el movimiento, se presentarán los distintos modos propios de oscilación y los desplazamientos transversales tendrán su máxima amplitud.

Para encontrar las frecuencias fn correspondientes a los modos propios de oscilación se utilizan las siguientes condiciones de frontera:

• ψ (0,t)=0

• ψ (L,t)=0

De la primera condición de frontera se obtiene (reemplazando en la ecuación 1):

[Asen k(0) + B cos k(0)] senωt = B senωt = 0

Por lo tanto B = 0 y la ecuación (1) queda de la siguiente manera:

ψ (x, t) = A sen kx senωt

De la segunda condición de frontera se obtiene:

Asen(Kl) sen(ωt) = 0

En esta ecuación A y senωt deben ser diferentes de cero. Por tanto:

Sen( kL) = 0

Lo cual es válido para kL = n Π con n = 1, 2, 3...

Figura 1: Ondas estacionarias en la cuerda.

Utilizando las expresiones del movimiento ondulatorio

k = 2 Π/λ 

y v = λ*f 

donde k y v son el número de onda y la velocidad de propagación de la onda respectivamente, se obtiene la siguiente expresión para las frecuencias correspondientes a los modos propios de oscilación de la cuerda:

fn =nv / 2L

De la dinámica asociada a las ondas transversales en una cuerda, la velocidad de propagación de ellas a lo largo de la misma está dada por:

v = √(F/ μ)

Siendo F la fuerza o tensión en la cuerda.

La expresión para las frecuencias propias queda en definitiva:

fn =(n / 2L) √(F/ μ) (3)

n = 1 corresponde al modo fundamental:

f1 =(1/2L) √(F/ μ)  

n = 2 corresponde al segundo armónico,

n = 3 al tercero y así sucesivamente, siendo cada uno de ellos múltiplos de la frecuencia fundamental en la forma:

f2 =2f1,

f3 = 3f1 ...

y así sucesivamente.

También n es el número de vientres de las ondas estacionarias como se muestra en la Figura 1.

Cuestionario ACTIVIDAD 2

El cuestionario consta de 17 numerales, los cuales pueden resueltos después de realizar las consultas indicadas y el laboratorio virtual indicado.

1. ¿Cómo puede calcular la densidad de una cuerda que vibra?  

2. ¿Cuál es la diferencia entre ondas estacionarias y ondas viajeras?

3. Explique gráficamente los modos de resonancia de una cuerda fija en ambos extremos.

4. Considérese una cuerda de longitud constante L que está vibrando en el modo fundamental o en el segundo armónico, ¿cómo es la relación entre frecuencia f y tensión F?

5. Considérese una cuerda con una tensión constante aplicada F que está vibrando en el modo fundamental o en el segundo armónico constante, ¿cómo es la elación entre la frecuencia y la longitud?

6. Construya en papel milimetrado una gráfica de frecuencia f en función del número de vientres n. ¿Qué clase de curva obtiene? ¿Cómo varía la frecuencia en función de los vientres?

7. Si la gráfica en el numeral anterior es una línea recta, ¿cómo obtendría el valor de la densidad de masa μ?  

8. Determine la densidad de la cuerda mediante la expresión:

μ =m / ℓT

Donde:

m es la masa de la cuerda

ℓT la longitud total de la cuerda

9. Compare en términos de porcentaje el valor de μ obtenido en los pasos 7 y 8

10. Construya un gráfico de frecuencia f en función de la tensión F. ¿Cómo es esta relación?

11. Construya un gráfico en papel milimetrado de frecuencia f en función de 1/L. ¿cómo es esta relación?

12. ¿cómo es la variación de la frecuencia respecto a la longitud de la cuerda?

13. ¿cómo escribiría la relación de comportamiento de la frecuencia en función de las variables discutidas en los pasos anteriores?

14. Cuando la cuerda está en resonancia, ¿por qué permanece finita la amplitud de vibración?

15. Cite fenómenos y aplicaciones donde se presenten ondas estacionarias.

16. Algunos cantantes pueden romper un vaso de vino al mantener cierto tono de voz. ¿Cómo se puede explicar esto?

17. Mediante diagramas explique los modos de resonancia de una cuerda fija en ambos extremos  

Forma de realización: registrar en papel con letra a mano, excelente presentación, buena ortografía y redacción, extensión máxima por término: tres renglones por cada uno.

Modalidad: grupal 

Forma de entrega: registrar en papel con excelente presentacion, a mano y  además socializar en el aula de clase.

Fecha máxima de entrega: la acordad en el salon de clase

NOTA: es recomendable realizar cada actividad dentro de la fecha establecida, ello implica un poco de auto-disciplina, un poco de responsabilidad y un poco de interés; además ayuda al estudiante para mejorar su capacidad de interpretar apropiadamente la información y adquirir nociones generales con cierta claridad sobre los temas programados, fortalecer su autonomía, su organización, su administración adecuada del tiempo y lograr mejor rendimiento académico en su proceso en general. 

BIBLIOGRAFIA

(1) FISICA volumen II: campos y ondas Alonso-Finn, sección 22.5

Además los textos referenciados en el tema Bibliografía los cuales se encuentran en la biblioteca de la institución

WEBGRAFÍA

los sitios referenciados en Webgrafía Actividad 1

xtr-10,2